Propiedades
De forma general si tenemos que el radio de la circunferencia circunscrita es ru
o también:
Perímetro[editar]
Siempre que supongamos que el pentágono tiene lado a:
ó también:
Para obtener el perímetro P de un pentágono regular, multiplíquese la longitud t de uno de sus lados por cinco (el número de lados n del polígono).
Fórmula para calcular los ángulos interiores[editar]
La suma de los ángulos internos de un pentágono es de 540°.
La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es:
El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5):
Construcción de un pentágono regular[editar]
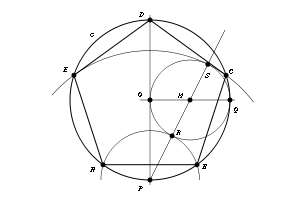
Podemos construir con regla y compás un pentágono regular, inscrito en una circunferencia (véase la figura) de la siguiente manera:
- Trazamos dos rectas perpendiculares por el centro O de la circunferencia (PD y OQ en la figura). Determinamos el punto medio M del segmento OQ y trazamos la recta PM. Con centro en M, trazamos la circunferencia de radio MO. Denotemos con R y S las intersecciones de esta circunferencia con la recta PM. Las circunferencias de centro en P y radios PR y PS determinan los vértices del pentágono regular.
Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él. En el centro quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.



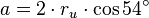


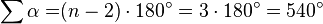
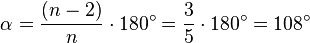

No hay comentarios:
Publicar un comentario